|
Reference and Fun Stuff
Composers A-Z |
|
Miscellaneous |


Music Theory
This page is basically for music theory. Pretty self-explanatory. Enjoy!
Intervals
What is an interval?
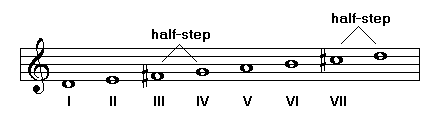
Numerical Size of Intervals
By counting the number of notes in an interval we obtain its numerical size. The first and last note must be counted. For example from C to E we have a third (C-1, D-2, E-3). In the next figure you can see the relationship between the number of notes and the numerical size of intervals:
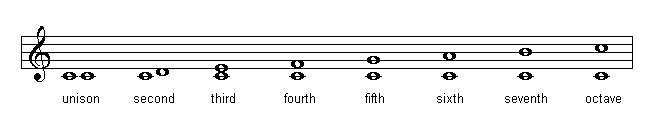
Yet, not all intervals of the same numerical classification are of the same size. That is why we need to specify the quality by finding the exact number of whole and half steps in the interval.
Whole and Half Steps
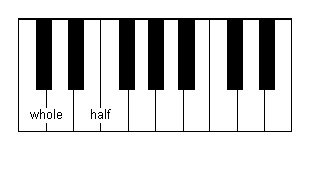
In the equal temperament tuning system the octave is divided exactly in twelve notes. The distance between each note is known as a half step. On the keyboard any key is at the distance of a half step from the next and previous key:
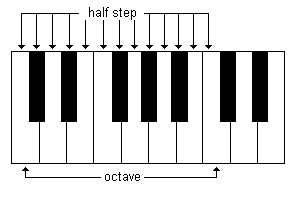
A whole step contains two half steps. All the white keys on the keyboard separated by a black key are at a distance of a whole step. The keys that are not separated by a black key are at a distance of a half step:
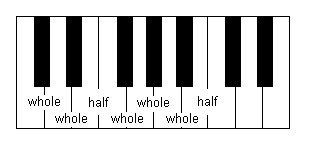
Notes corresponding to the white keys on the keyboard are called C, D, E, F, G, A and B. These notes are considered natural notes. They can be raised a half step with a sharp or lowered with a flat. A black key, for example the one between C and D, can be considered a C sharp or a D flat:
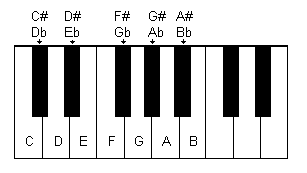
Interval Quality
By using the keyboard to count the number of half steps between notes we can see that intervals with the same numerical classification can contain a different number of half steps. For example, the second between C and D has one whole step while the second between E and F has only one half step:
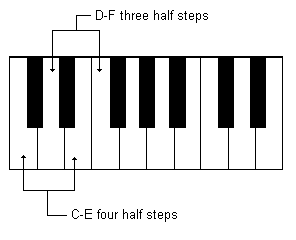
The same thing happens with other intervals. For example the third D-F has 1½ whole steps or 3 half steps while C-E has 2 whole steps or 4 half steps:
This is the reason why we need to specify the quality of an interval. Please refer to each interval for more information.
Seconds
Seconds can be major, minor, augmented or diminished. Below you can see the number of half steps according to the quality of a second:

Diminished second, 0 half steps

Minor second, 1 half step

Major second, 2 half steps or one whole step
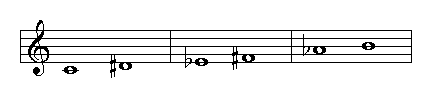
Identifying Seconds
Seconds are probably the easiest intervals to identify. Yet, it is very important to master the identification of seconds since it will be used when identifying other intervals.
To identify the quality of a second we must know:
-the number of half steps contained in each type of seconds
-the order of musical notes (C, C#-Db, D, etc.). We must remember that between all natural notes, with the exception of E-F and B-C, there is a distance of one whole step.
With this in mind, we can count the number of half steps in a second:

Another Way of Identifying Seconds
If both notes are natural, we don't have to count the number of half steps if we remember that only the seconds E-F and B-C are half steps. If there are accidentals, we can use the following method:
-Make all notes natural and determine the quality.
-Add the accidentals and see how the interval is affected.
Example: G#-A#:
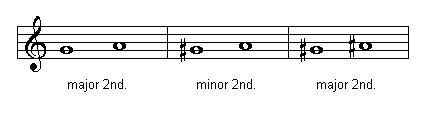
-Make all notes natural. G-A is a major 2nd. (only E-F and B-C are minor).
-Add a sharp to G. The interval is now smaller, it becomes a minor 2nd.
-Add a sharp to A. The interval is now larger, it becomes a major 2nd.
Another example: C#-D double sharp:
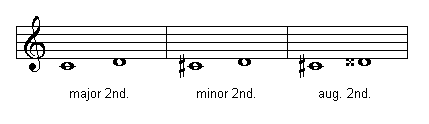
-Add a sharp to C. The interval is now smaller, it becomes a minor 2nd.
-Add a sharp to D. The interval is now larger, it becomes a major 2nd.
-Add a second sharp to D. The interval is now even larger, it becomes an augmented 2nd.
Thirds
Thirds can be major, minor, augmented and diminished. Below you can see the number of half steps according to the quality of a third:

Diminished third, 1 whole step or 2 half steps

Minor third, 1 1/2 whole steps or 3 half steps

Major third, 2 whole steps or 4 half steps
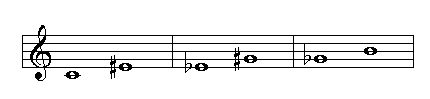
Identifying Thirds
A third can be identified by analyzing the seconds between the lower and higher notes and a middle note inside the third. For example, the third C-E has two seconds: C-D and D-E. Using the following table we can find out the quality of the third:
If any note has accidentals, we can determine the quality of the interval without accidentals and then analyze the effect of the accidentals:
Example: Ab-Cb:
Following this method we find that the third C-E is a major third because both seconds (C-D, D-E) are major seconds.

-Make all notes natural. A-B is a major second, B-C is a minor second, so A-C is a minor 3rd.
-Add a flat to A. The interval is now a major third.
-Add a flat to C, the interval is now a minor third.
Other Ways of Identifying Thirds
-Learning the number of steps for each type of third and counting the whole and half steps.
-Associating thirds with scales, triads, etc. For example the third D-F# can be associated with the I and III degrees of the D Major scale or with the third of the D Major triad. If we know that the third from the I to III degrees in major scales and the third of a major chord are major, we know then that D-F# is also a major third.
Fourths
Fourths can be perfect, augmented or diminished. Below you can see the number of steps according to the quality of the interval:
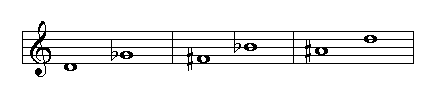
Diminished fourth, 2 whole steps or 4 half steps

Perfect fourth, 2 1/2 whole steps or 5 half steps

Identifying Fourths
When analyzing the quality of a fourth we should know that:
-The interval is a perfect fourth if all the notes are natural with the exception of the fourth F-B which is an augmented fourth.
-If there are accidentals you should identify the interval without accidentals and then analyze the effect of the accidentals.
Example: G-C#:
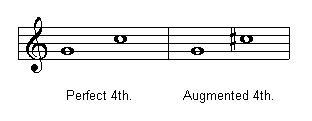

Identifying fourths by counting whole and half steps is slow and confusing.
Fifths
Fifths can be perfect, augmented or diminished. Below you can see the number of steps according to the quality of the interval:
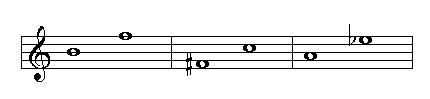
Diminshed fifth, 3 whole steps or 6 half steps

Perfect fifth, 3 1/2 whole steps or 7 half steps
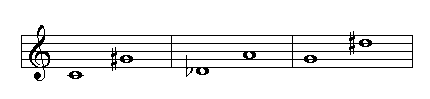
Identifying Fifths
When analyzing the quality of a fifth we should know that:
-the interval is a perfect fifth if all the notes are natural with the exception of the fifth B-F which is a diminished fifth.
If there are accidentals you should identify the interval without accidentals and then analyze the effect of the accidentals.
Example: D-A#:

Another example: Gb-Db:

Identifying fifths by counting whole and half steps is slow and confusing.
Sixths
Sixths can be major, minor, augmented or diminished. Below you can see the number of steps according to the quality of the interval:
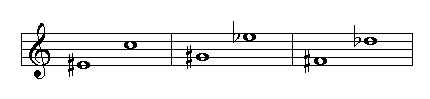
Diminished sixth, 3½ whole steps or 7 half steps

Minor sixth, 4 whole steps or 8 half steps

Major sixth, 4½ whole steps or 9 half steps

Augmented sixth, 5 whole steps or 10 half steps
The easiest way to identify the quality of a sixth is by inverting the interval and identifying the resulting third. For example, the interval C#-A#:
-The inversion is A#-C#.
-We identify the resulting third.
-A#-C# is a minor 3rd. so C#-A# is a major 6th.

A major 6th. becomes a minor 3rd. when inverted
Sevenths can be major, minor, augmented or diminished. Below you can see the number of steps according to the quality of the interval:

Diminished seventh, 4½ whole steps or 9 half steps

Minor seventh, 5 whole steps or 10 half steps

Major seventh, 5½ whole steps or 11 half steps
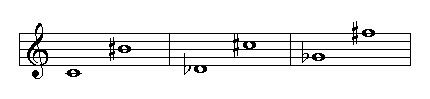
Augmented seventh, 6 whole steps or 12 half steps
The easiest way to identify the quality of a seventh is by inverting the interval and identifying the resulting second For example, the interval C-B:
-The inversion is B-C.
-We identify the resulting second.
-B-C is a minor 2nd. so C-B is a major 7th.

A major 7th. becomes a minor 2nd. when inverted
Octaves can be perfect, augmented or diminished. Below you can see the number of steps according to the quality of the interval:

Diminished octave, 5½ whole steps or 11 half steps

Perfect octave, 6 whole steps or 12 half steps

Augmented octave, 6½ whole steps or 13 half steps
The easiest way to identify sixths and sevenths is by inverting the interval and analyzing the resulting third or second.
For example, instead of counting the number of whole and half steps in the sixth F#-D#, you can invert the interval and analyze the resulting third. Since the third D#-F# is a minor third, the sixth F#-D# is a major sixth.See Inversion of Intervals for more information about how the intervals are transformed after inversion.
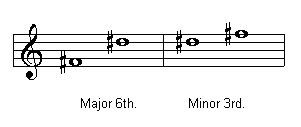

Note pitches can be modified by using accidentals:
| Accidental | Name | Effect |
| sharp | Raises the note 1 half step | |
| flat | Lowers the note 1 half step | |
| double sharp | Raises the note 2 half steps or 1 whole step | |
| double flat | Lowers the note 2 half steps or 1 whole step | |
| natural | Cancels any previous accidental |
Intervals can be classified as consonant or dissonant according to the complexity of the mathematical relation between the notes pitches.
Although this concept has changed during musical history and even today not all theoreticians agree, we can offer the following classification:
Consonance and Dissonance
|
| |
Major and Minor Third Perfect Fourth Perfect Fifth Major and Minor Sixth Perfect Octaves | Seventh Augmented Fourth Diminished Fifth |
Notes with the same pitch but different names are called enharmonic. G#-Ab are enharmonic notes.
Enharmonic

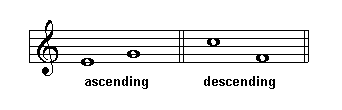
Ascending and Descending Intervals
When the second note of an interval is higher than the first note the interval is an ascending interval. If the second note is lower the interval is a descending interval.
Compound and Simple Intervals
Simple intervals are not bigger than an octave while compound intervals are larger than an octave.
Ninths, tenths, elevenths and thirteenth are examples of compound intervals.
Sometimes we simplify compound intervals and refer to them using the corresponding simple interval:
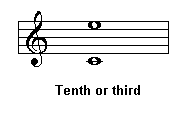
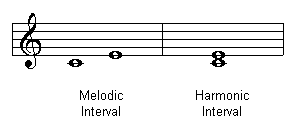
Melodic and Harmonic Intervals
In a harmonic interval both notes are sounded simultaneously. In a melodic interval notes are played in succession.
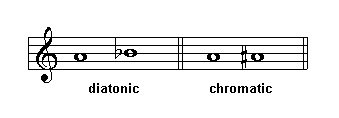
Chromatic and Diatonic Half Steps
In a chromatic half step both notes have the same name, for example A-A#. In a diatonic half step notes have different names, for example A-Bb:
The Tritone
A tritone is an interval that contains three whole steps:
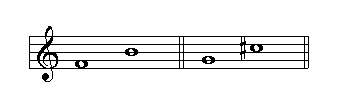
Unison
Two notes of the same pitch and name are said to be in unison:

Mathematics Relation of Intervals
The A above middle C, normally has a frequency of 440 cycles per second or Hertz. This means that it vibrates 440 times per second. An A, one octave higher has a frequency of 880 Hz., exactly the double of vibrations per second. The mathematics expression of this relation is 880:440 or 2:1. The following table shows the mathematical relation of several intervals, ordered from consonant to dissonant.
Scales
What is a scale?
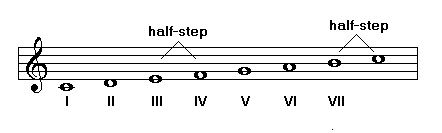
According to the equal temperament tuning system, octaves are equally divided into twelve notes. A scale is a series of notes selected among these twelve notes.
Each of these notes is called a degree. Each degree has its own name but is also often designated by a Roman numeral:
Two scales are distinguished from one another by:
-The number of notes they have
-The distance between their degrees.
For example, seven different scales may be built with the seven natural notes as in the following examples:
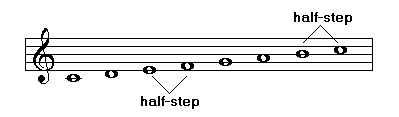

Each of these scales has a characteristic order of whole steps and half-steps. The first one is called major scale, the second one Third Gregorian mode or Phrygian mode. Those names refer to the specific structure of each scale.
A scale may be built starting with any note using accidentals in order to maintain the order of whole steps and half-steps. For instance, in order to build a major scale on note D, F and C have to be altered:
Scale of D Major
Such a scale is called the major scale of D. It is major because of its structure and a scale of D because D is the note upon which it is formed.
There is an infinity of scales. Scales may also be created while composing. Composers such as Claude Debussy, Olivier Messiaen, and Bela Bartok, among others, have done so in the recent past.
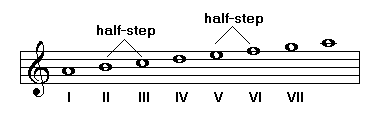
The Major Scale
The major scale has 7 notes. Notes are separated from one another by one whole step except for degrees III-IV and degrees VII-I:

The major scale and the minor scale are the most common scales because they have been constantly used for the past four centuries.
The Minor Scale
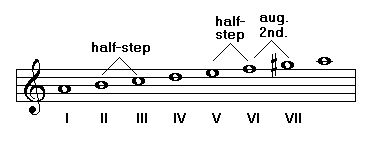
As the major scale, the minor scale has 7 notes. However, it has three variants: the natural minor, the harmonic minor, and the melodic minor. Those variants differ in the manner degrees VI and VII are altered.
In the natural minor scale, all notes appear with the same accidentals as in its relative major. Hence the name of natural:
Minor Natural Scale
Half-steps are found between degrees II-III and V-VI.
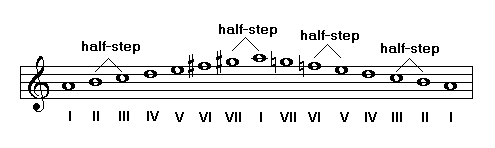
The degree VII of a minor scale is very often raised. The resulting scale is referred to as harmonic minor scale because the raising of degree VII is often harmonically motivated. Raising that note forms the dominant chord or dominant seventh chord on the fifth degree of the scale:
Minor Harmonic Scale
Besides raising degree VII, degree VI may also be altered. The resulting scale is called melodic minor scale. The main purpose of this accidental is to facilitate the melodic movement from degree VI to degree VII, avoiding the augmented second that is formed in the harmonic minor scale. Therefore, it is referred to as the minor melodic scale:
Minor Melodic Scale
Relative Scales
The major scale of C and the natural minor scale of A contain the same notes. They are relative scales. C is the relative major of A, and A is the relative minor of C:
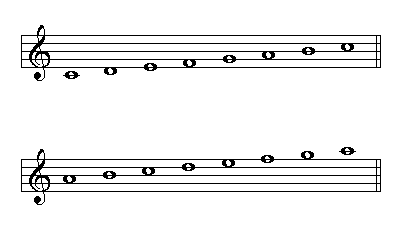
Scales of C Major and A Minor
In order to identify the relative minor of a major scale, its degree VI has to be identified. For instance, the relative minor of F major is its degree VI, D.
As for relative majors, degree III has to be identified. For instance, the relative major of C minor is its degree III, E flat.
Key Signatures
Major and natural minor scales built on C and A respectively do not contain any altered note. In order to build these scales starting from any other note, it is necessary to alter one or more notes. For instance, in the scale of G major, note F is sharp. If you wished to write a melody in G major, you would need to alter all F notes. Key signatures are used to avoid writing so many accidentals.
Key signatures are placed at the beginning of each staff, between the clef and the meter signature:

Key of G Major
In the former melodic fragment, all F are sharp. Therefore, if you want to write a natural F, it should be preceded by a natural.
Scales with sharps in their key signatures are the following:
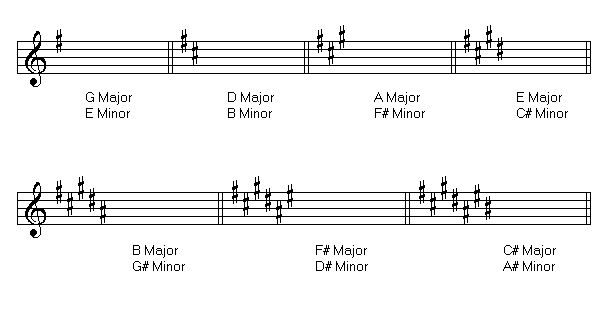
Scales with flats in their key signatures are the following:
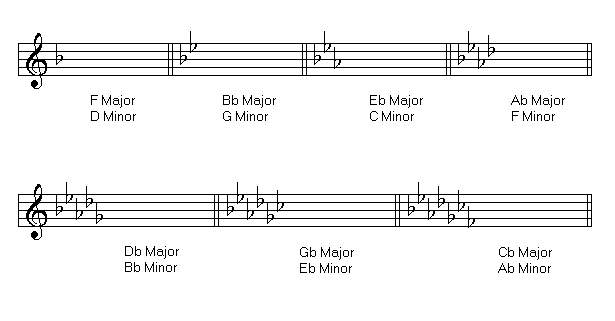
Identifying Key Signatures
Each key signature is related to a major scale and its relative minor. With practice, it is possible to memorize the accidentals that are typical of each scale. Meanwhile, key signatures may be identified and built otherwise.
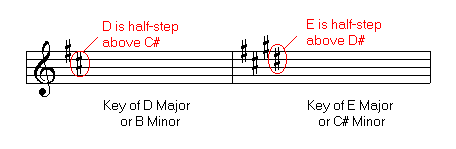
Identifying Key Signatures of Sharps
The major scale to which it belongs is a half-step above the last sharp.
Identifying Key Signatures of Flats
The major scale to which it belongs is a perfect fourth below the last flat. In case of more than one flat, tonality is also indicated by the penultimate flat.
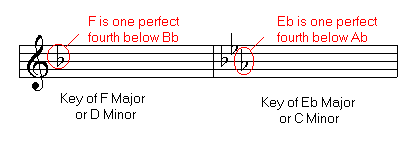
-Building Key Signatures-
Major Scales
In order to build the key signature of a major scale or tonality, it is important to remember that the major scale of C does not have any key signature. On the contrary, any other scale may have sharps or flats.
All major scales based on a flat note, G flat, E flat, D flat, etc. use key signatures with flats. The only exception is F major. Therefore, when you are looking for a key signature, you can assume that it uses sharps if it is not F or does not begin with a flat note:
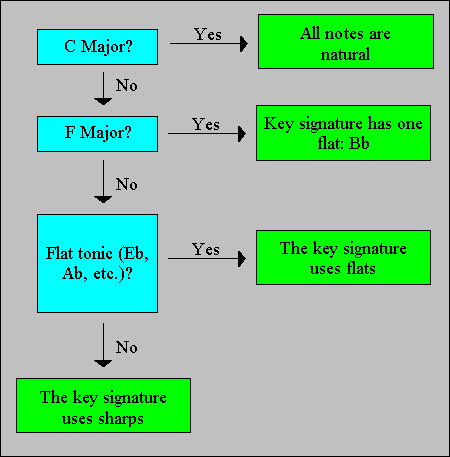
Once the accidentals used in the key signature are known, the following procedure may be used to build the key signature:
Building Key Signatures of Sharps
Follow the order of the sharps until you reach the one that is a half-step below the major scale chosen. For instance, A major, F#, C#, G#. G# is a half-step below A. Therefore, sharps are F#, C#, G#.
Building Key Signatures of Flats
Follow the order of the flats until you reach the one following the one that bears the same name in the major scale chosen. For instance, A flat major, B flat, E flat, A flat, D flat. D flat comes after A flat; therefore, flats are B flat, E flat, A flat, and D flat.
This method does not apply to the major scale of F that has a flat. Therefore, this key signature has to be memorized.
Building Key Signatures of Minor Scales
In the case of minor scales, the relative major has to be identified. Two relative scales have the same key signatures.
Names of Degrees
Besides referring to the degrees of the major and minor scales by Roman numbers, the following names may also be used:
The concept of tonality came into being during the Renaissance and was established during the Baroque period. It is related to the use of major and minor scales.
When a piece is built on a major or minor scale, the tonic of this scale becomes the tonal center. The piece is based on this note: the piece is in the tonality or key related to this scale. For instance, if the scale is a major scale of D, the key is D major.
In the musical pieces written during the Baroque, Classical, and Romantic period, key is meant as the main key. However, numerous modulations (momentary changes of keys) occur throughout the piece.
Chords and, in particular, chords of the dominant seventh, and harmony help define tonality and modulation processes.
Gregorian modes were used during the Middle Ages and the Renaissance. During the Renaissance, they progressively became our major and minor scales. The number of modes varies according to the time period and the theorist, but in general, eight Gregorian modes have been identified.
Gregorian modes had a final, a note with which the melody ended and on which it was based. Its function was similar to that of the tonic in the major and minor scales. Furthermore, Gregorian modes had a dominant. The dominant was a note upon which there was much insistence throughout the melody.
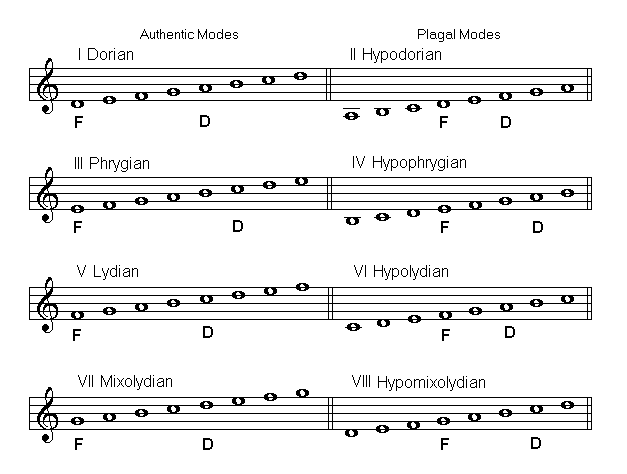
Modes are divided into two categories: authentic modes and plagal modes. Each plagal mode is associated with an authentic mode. Both have the same notes and the same Final. The difference between an authentic mode and its related plagal lies in the nature of the dominant note and in the range.
Treatises on Gregorian Chant assign the odd numbers I, III, V, and VII to authentic modes. Their related plagal modes are assigned the even numbers, II, IV, VI, and VIII. The related plagal mode of the authentic mode I is II, that of III is IV, etc.
Some theorists use Greek names such as Dorian, Phrygian, Lydian, and Mixo-Lydian to refer to the authentic modes I, III, V, and VII respectively. As for plagal modes, the prefix hypo is added to the name of its authentic relative: mode II becomes the Hypo-Doric mode, mode IV the Hypo-Phrygian one, etc.
Those modes have been forgotten for several centuries. However, variants have come back and have been used again in Classical music as well as in jazz.
The eight Gregorian modes are listed below. Finals are indicated with the letter F, dominants with the letter D:
Tonality
Gregorian Modes
Jazz Modes
The following modes that are variants of the Gregorian modes are used in jazz nowadays and have been used since the end of the past century by composers such as Claude Debussy. Some of these modes have survived in folk music in some regions; this is the case of the Phrygian mode in Andalusian music:
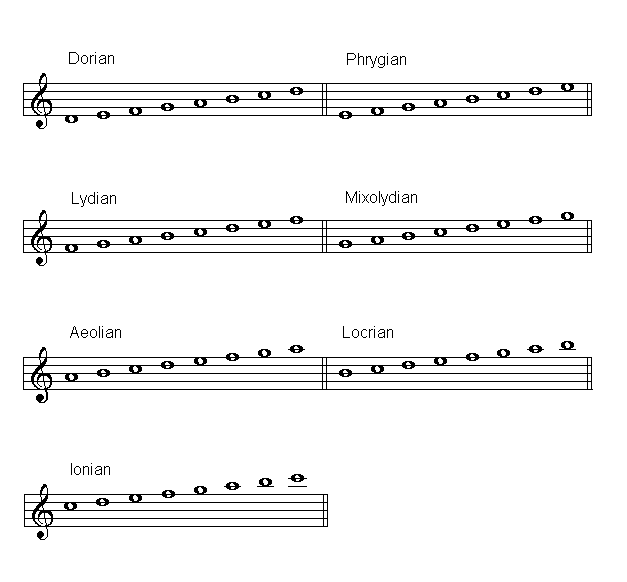
To see more modes and scales used in Jazz read The Art of Improvisation for Classical Guitarist by Jacques Landry.
Pentatonic Scales
Pentatonic scales are scales formed of five notes (from the Greek pente: five). These scales have been very much used in the folk music of various countries. More recently, composers such as Claude Debussy and Maurice Ravel have used them in their music.
Although any scale formed of five notes may theoretically be called pentatonic, the most common forms are the following:

Those two types of pentatonic scales may be related to major and minor scales. The first one looks like a major scale without degrees IV and VII. The second one looks like a minor scale without degrees II and VI. Both contain the same notes but differ by their tonic. Because of this similarity, some theorists have named them major pentatonic and minor pentatonic.
The Chromatic Scale
The chromatic scale contains twelve notes separated from one another by a half-step.

Whole-Tone Scale
The whole-tone scale has six notes separated from one another by a whole step. Several examples of the whole-tone scale are found in Claude Debussy's work:

The Diminished Scale
The diminished scale consists of eight notes. Distance between notes may be a whole step or a half-step. The term diminished comes from the fact that degrees I, III, V, and VII form a chord of diminished seventh.
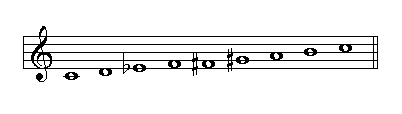
Chords
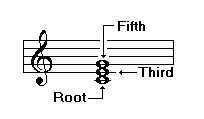
What is a Chord?
Three or more notes simultaneously sounded form a chord. Traditionally, chords have been built by superimposing two or more thirds. For example, notes C-E-G form a chord or major triad. The note upon which the chord is founded is called the root. The other notes are called by the name of the interval they form in relation to the root:
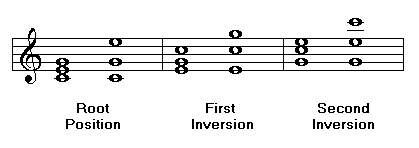
Inversions
A chord is said to be in its root position when its root is the lowest note. A three-note chord or triad may also stand in its first or second inversion. A chord stands in its first inversion when its third is the lowest note. It is in second inversion when its fifth is the lowest note. In the following example, the major triad of C stands in its root position and first and second inversion respectively:
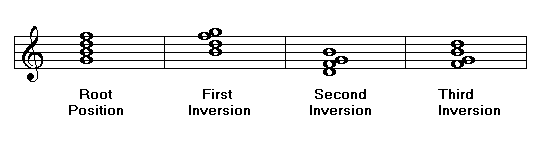
The more notes a chord has, the more inversions it may have. In the following example, the dominant seventh chord of G is presented in its four positions:
Triads
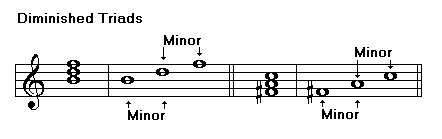
Triads are chords formed of three notes. Triads may be major, minor, augmented, or diminished. The following examples show the structure of each of these chords:
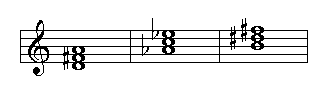
Major triad, major 3rd., perfect 5th
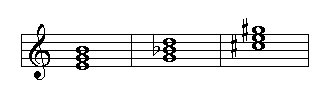
Minor triad, minor 3rd., perfect 5th
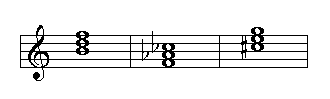
Diminished triad, minor 3rd., diminished 5th
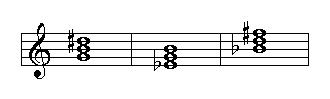
Augmented triad, major 3rd., augmented 5th
Forming Triads in Major Scales
The following examples show triads that may be formed by using the notes of a major scale:
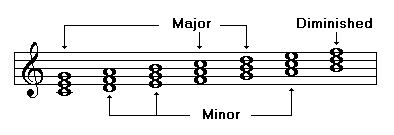
In all major scales, triads that are formed on degrees I, IV, and V are major. Those formed on degrees II, III, and VI are minor; the triad formed on degree VII is diminished.
Forming Triads in Minor Scales
The variety of triads in minor scales is greater because there are three types of minor scales: natural, harmonic, and melodic.
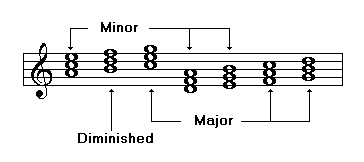
Triads in the minor natural scale
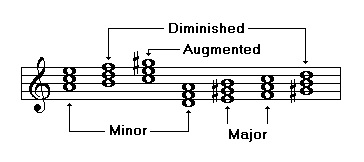
Triads in the minor harmonic scale
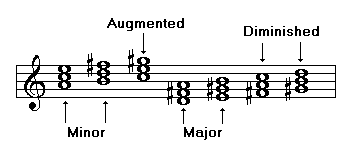
Triads in the minor melodic scale
Triads and Scale Degrees
The following table shows the scale degrees where we find each type of triad:
Identifying triads quickly and accurately is an essential requirement if you want to be able to analyze and understand the music you interpret or to which you listen. Therefore, it is important to develop that skill which involves being able to identify intervals and particularly thirds and fifths.
Using your knowledge about intervals, you can identify triads quickly. One way to do it is identifying the third and then the fifth. The following table shows the combination of intervals that is characteristic of each type of triad:
Knowing the type of triad formed on each scale degree may be very helpful when identifying triads.
Identifying Triads
 | |||
 | |||
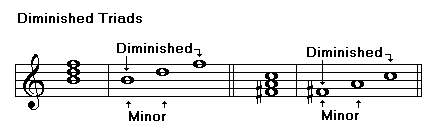 | |||
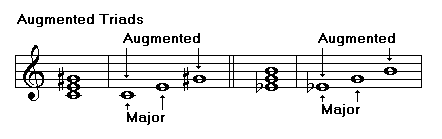 |
You can also identify the two thirds building the chord. The following table shows the combination of intervals characteristic of each type of triad:
 | |||
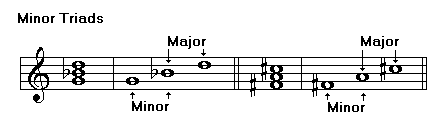 | |||
 | |||
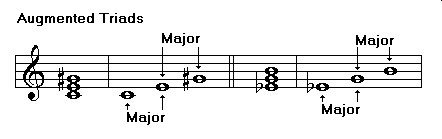 |
Knowing well the type of triad built on each scale degree can help you identify triads rapidly.
A few examples:
1. First, you can notice that the key is A major. A triad built on the third degree of major scales is minor; however, here, the third of the chord has become a major third since it was raised. Therefore, the triad is major.
If you add a third to any triad, you obtain a seventh chord. This chord is called seventh chord because a seventh interval is formed in relation to the root.
Seventh chords may be built on each of the degrees of major and minor scales. Seventh chords may be identified by analyzing the triad and the seventh interval forming the chord.
The following examples show the structure and examples of the most common seventh chords:
Alternative for Identifying Triads

D major. Here, the key is G major. The chord is formed on the fifth degree of the scale. Triads built on the fifth degree of major scales are major.

C minor . Here, the key is B flat major. The chord is formed on the second degree. Triads built on the second degree of major scales are always minor triads.

C# major . Here, there are two ways of identifying the type of triad.
2. Or you can also notice that the key is F# minor. E# is characteristic of harmonic and melodic minor scales. Therefore, in both cases, the chord built on the fifth degree is major.
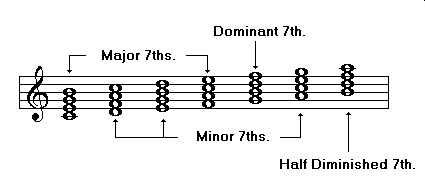
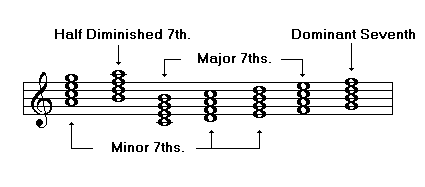
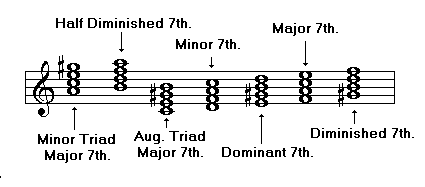
Seventh Chords

Dominant Seventh: major triad, minor 7th

Half Diminished Seventh: diminished triad, minor 7th

Major Seventh: major triad, major 7th

Minor Seventh: minor triad, minor 7th

Diminished Seventh: diminished triad, diminished 7th
Knowing the origin of the names given to the chords helps you remember their structure:
The following examples show the seventh chords that may be formed by using a major scale:
As shown on the table above, dominant sevenths are called by the name of the scale degree on which they are formed. The name given to major, minor, and diminished sevenths is determined by the type of triad and seventh interval on which they are built.
Forming Seventh Chords in Major Scales
Seventh Chords in Major Scales
Forming Seventh Chords in Minor Scales
Since there are three types of minor scales (natural, harmonic, and melodic), there is a greater variety of seventh chords in these scales.
Seventh Chords in the Minor Natural Scale
Seventh Chords in the Minor Harmonic Scale
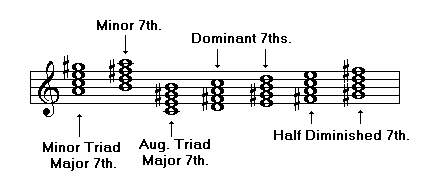
Seventh Chords in the Minor Melodic Scale
Seventh Chords and Scale Degrees
The following table shows the scale degrees where we find each type of seventh chord:
Knowing the type of sevenths found in each scale degree may be useful when identifying seventh chords.
There are two ways of identifying seventh chords.
First, the triad and the seventh intervals forming the chord may be identified. In order to use this method, the structure of each of the different types of seventh chords should be known:
Identifying Seventh Chords
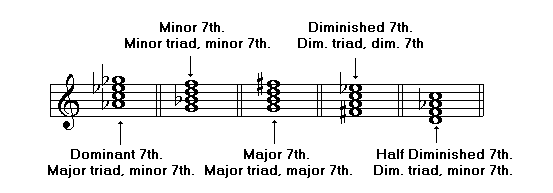
Otherwise, the type of chord may be identified by determining the key and the degree on which the chord is built:

Dominant Seventh. The key is D-major and the chord is built on the fifth degree. In the major keys, a chord of dominant seventh is built on the fifth degree.
For more information, refer to Identifying Triads.
Ninth Chords
A ninth chord is created by adding a ninth to a seventh chord.
The most common ninth chords are built on the dominant degree in minor keys as well as in major keys. Since the ninth formed is major in major keys and minor in minor keys, those chords are called major dominant ninths and minor dominant ninths.

Ninth chords may also be built on minor sevenths and major sevenths:
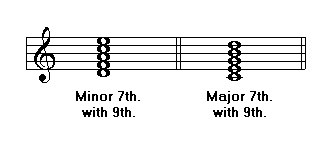
The augmented ninth chord is obtained by adding an interval of augmented ninth to a dominant seventh chord. In many occasions, the ninth interval is simplified enharmonically. In these cases, the chord seems to be a dominant ninth chord with a major and minor third:

As early as in Chopin's music, this chord is found in the form of an arpeggio:

Usually, this chord is not mentioned in harmony treatises.
Eleventh and Thirteenth Chords
Besides adding sevenths and ninths to triads, it is also possible to continue adding eleventh and thirteenth intervals. A triad to which the seventh, the ninth, the eleventh, and the thirteenth are added, will contain the seven notes of the scale:
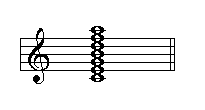
Due to the sound density, one or more notes are usually eliminated from these chords. It is also common to eliminate the third, in particular in the case of eleventh chords. The following examples show two examples of these chords:

Dominant 7th. chord with 9th. y 11th., C. Debussy, La fille aux cheveux de lin

Major chord with 9th., 11th. y 13th., C. Debussy, La fille aux cheveux de lin
The fifth is often raised and/or lowered in dominant seventh chords:

Chords with augmented and diminished fifths
Augmented Sixth Chords
There are at least three types of augmented sixths: the Italian sixth, the French sixth, and the German sixth. Those chords are generally used to reach the dominant or tonic chord in second inversion when performing a cadence in major and minor keys.
The Italian Sixth
The Italian Sixth chord is formed on the fourth degree. Most commonly, it is in first inversion. Its root is raised creating an augmented sixth interval with the bass:

Italian Sixth, A minor

Italian Sixth, A Major
The French Sixth
The French sixth is formed on the second degree. It is a seventh chord. Most commonly, it stands in its second inversion. Its third is raised in order to build an augmented sixth interval with the bass:

French Sixth, A minor

French Sixth, A Major
The German sixth chord is built on the fourth degree. It is a seventh chord. It is most commonly in the first inversion. Its root is raised in order to create an augmented sixth interval with the bass:

German Sixth, A Minor
Neapolitan Sixth
The Neapolitan sixth chord is built on the second degree of the major and minor scales. Generally, it is used in first inversion. Its root is lowered. It is commonly used to reach the dominant chord or the tonic chord in second inversion when performing a cadence:

Neapolitan Sixth, A Minor

Neapolitan Sixth, C Major